If there is one prayer that you should pray/sing every day and every hour, it is the LORD's prayer (Our FATHER in Heaven prayer)
It is the most powerful prayer. A pure heart, a clean mind, and a clear conscience is necessary for it. - Samuel Dominic Chukwuemeka

For in GOD we live, and move, and have our being. - Acts 17:28

The Joy of a Teacher is the Success of his Students. - Samuel Dominic Chukwuemeka



Word Problems on the Applications of Derivatives

SamDom For Peace Verify your answers as applicable with the: Differential Calculus Calculators

Prerequisite Topics:
Exponents and Logarithms
Factoring
Difference Quotient
Trigonometry
Derivatives

For JAMB Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

For WASSCE Students
Any question labeled WASCCE is a question for the WASCCE General Mathematics
Any question labeled WASSCE-FM is a question for the WASSCE Further Mathematics/Elective Mathematics

For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.

Solve all questions
Show all work
Use at least two methods whenever applicable
Indicate the method(s) used as applicable
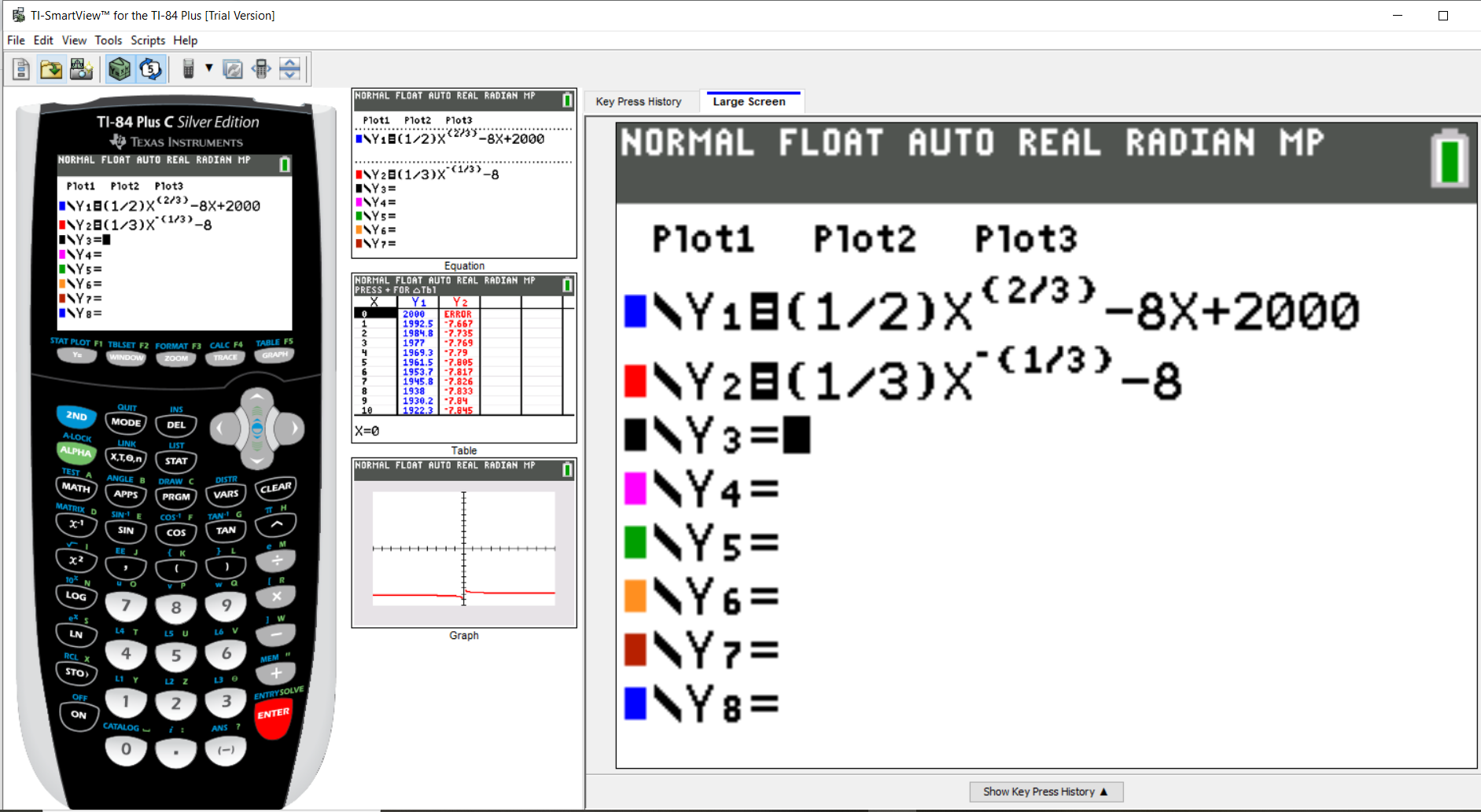
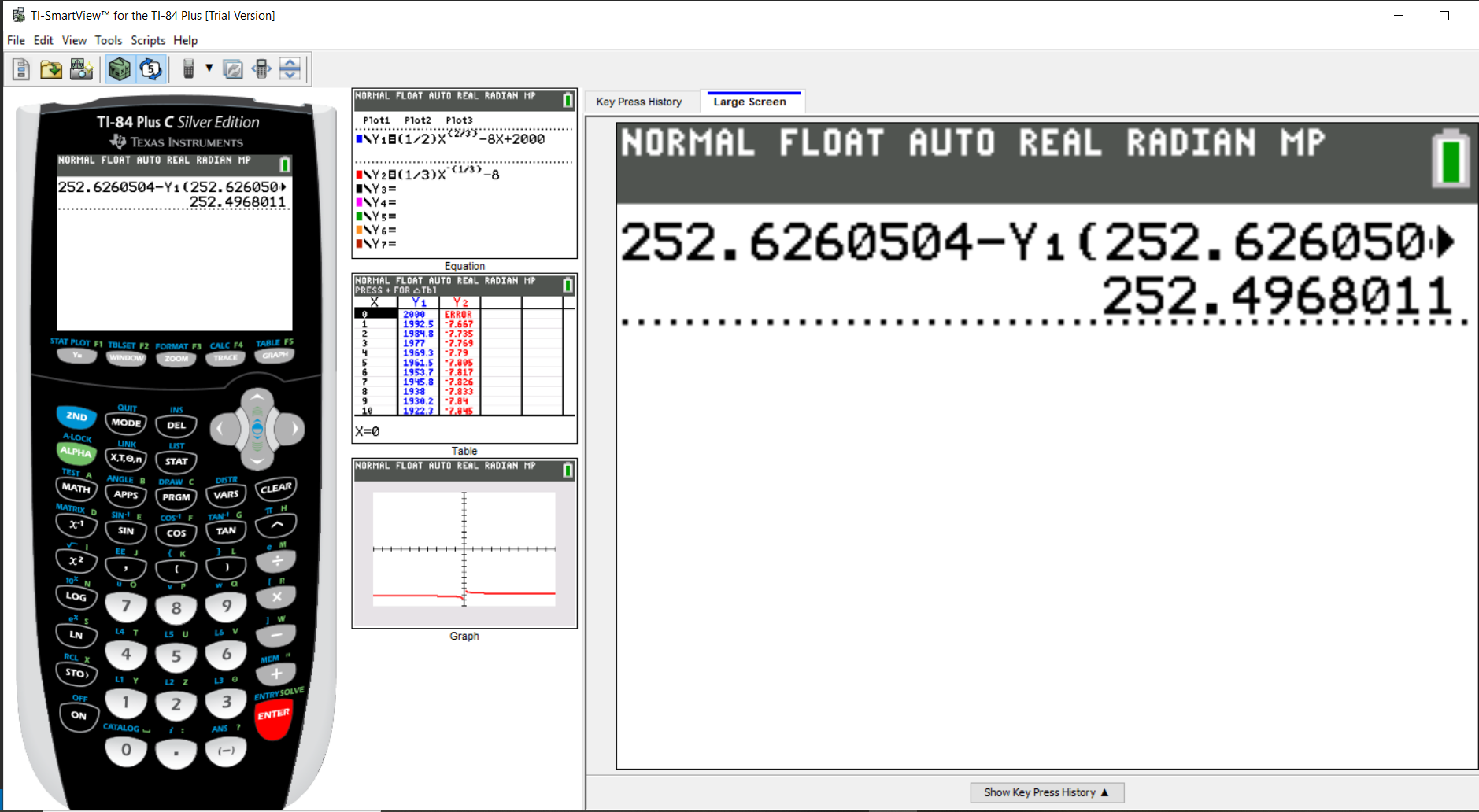
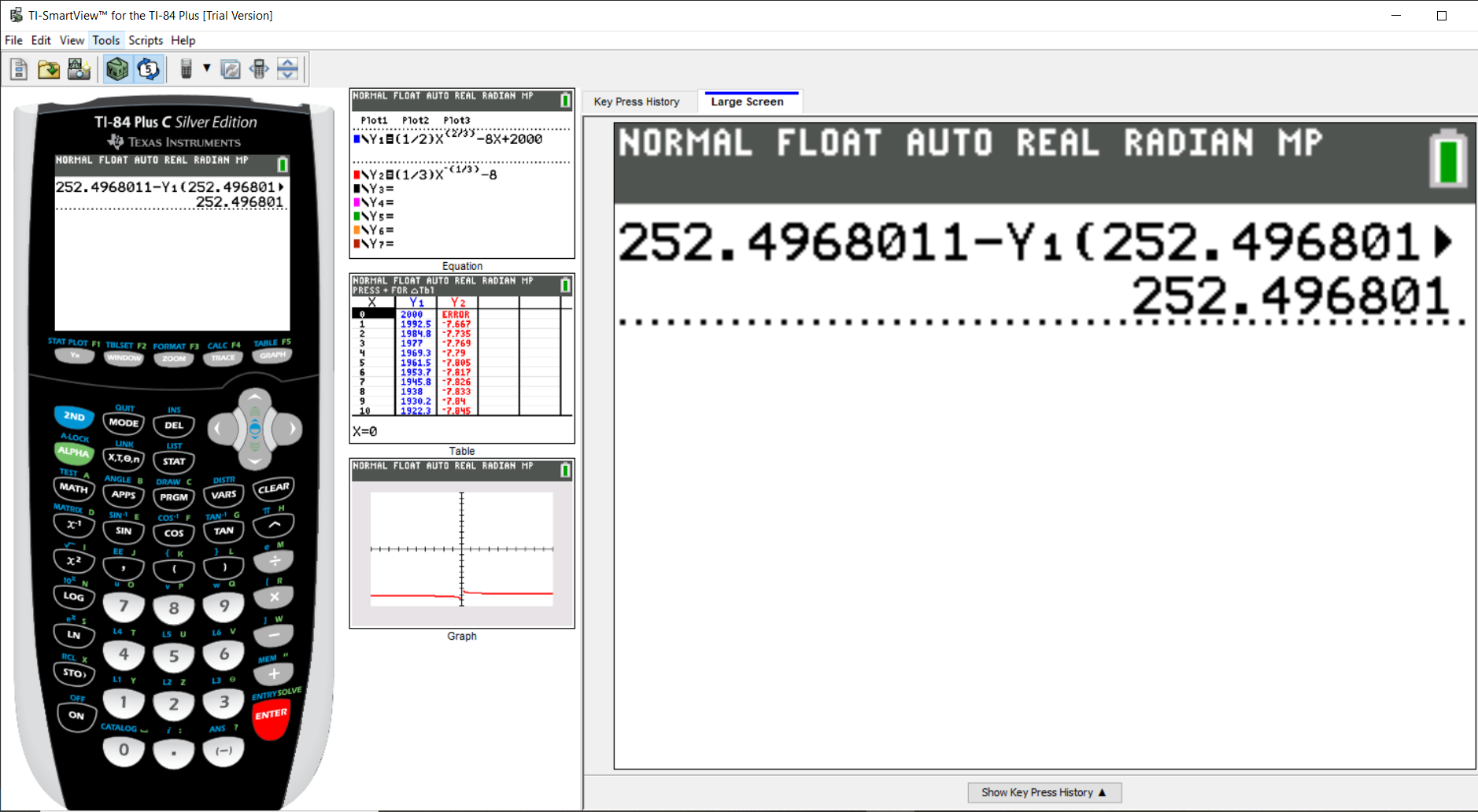
For questions involving Newton's method, you may use the TI-84 Plus calculator as illustrated in Example 2

(1.) Assume the cost for publishing a book is modelled by the function: $C(x) = 2000 + 14x + \dfrac{1}{2}x^{\dfrac{2}{3}}$

Use Newton's method to determine the break-even point if the selling price of the book is $22.00
Take the initial guess as 125
Round your answer to the nearest integer.


$ \underline{Break-even\;\;Point} \\[3ex] cost = revenue \\[3ex] cost = C(x) = 2000 + 14x + \dfrac{1}{2}x^{\dfrac{2}{3}} \\[7ex] revenue = R(x) = 22 * x = 22x \\[3ex] \implies \\[3ex] 2000 + 14x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 22x \\[7ex] 2000 + 14x - 22x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 0 \\[7ex] 2000 - 8x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 0 \\[7ex] \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 = 0 \\[7ex] \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 = f(x) \\[7ex] f(x) = \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 \\[7ex] f'(x) = \dfrac{2}{3}\left(\dfrac{1}{2}\right)\left(x^{\dfrac{2}{3}} - 1\right) - 8 \\[7ex] f'(x) = \dfrac{1}{3}x^{-\dfrac{1}{3}} - 8 \\[7ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = x_n - \dfrac{\dfrac{1}{2}x_n^{\dfrac{2}{3}} - 8x_n + 2000}{\dfrac{1}{3}x_n^{-\dfrac{1}{3}} - 8} \\[9ex] x_1 = 125 \\[3ex] x_2 = x_1 - \dfrac{\dfrac{1}{2}* x_1^{\dfrac{2}{3}} - 8 * x_1 + 2000}{\dfrac{1}{3} * x_1^{-\dfrac{1}{3}} - 8} \\[9ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 125^{\dfrac{2}{3}} - 8 * 125 + 2000}{\dfrac{1}{3} * 125^{-\dfrac{1}{3}} - 8} \\[9ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* (\sqrt[3]{125})^2 - 8 * 125 + 2000}{\dfrac{1}{3} * (\sqrt[3]{125})^{-1} - 8} \\[7ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 5^2 - 8 * 125 + 2000}{\dfrac{1}{3} * 5^{-1} - 8} \\[7ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 25 - 8 * 125 + 2000}{\dfrac{1}{3} * \dfrac{1}{5} - 8} \\[7ex] x_2 = 125 - \dfrac{12.5 - 1000 + 2000}{\dfrac{1}{15} - 8} \\[7ex] x_2 = 125 - \left(1012.5 \div -\dfrac{119}{15}\right) \\[5ex] x_2 = 125 - \left(1012.5 * -\dfrac{15}{119}\right) \\[5ex] x_2 = 125 - -\dfrac{15187.5}{119} \\[5ex] x_2 = 125 + 127.6260504 \\[3ex] x_2 = 252.6260504 \\[5ex] x_3 = x_2 - \dfrac{\dfrac{1}{2}* x_2^{\dfrac{2}{3}} - 8 * x_2 + 2000}{\dfrac{1}{3} * x_2^{-\dfrac{1}{3}} - 8} \\[9ex] x_3 = 252.6260504 - \dfrac{\dfrac{1}{2}* 252.6260504^{\dfrac{2}{3}} - 8 * 252.6260504 + 2000}{\dfrac{1}{3} * 252.6260504^{-\dfrac{1}{3}} - 8} \\[5ex] $
Number 1a

Number 1b

$ x_3 = 252.4968011 \\[3ex] $
Number 1c

$ x_4 = 252.496801 \\[3ex] x_4 \approx x_3...STOP \\[3ex] \implies \\[3ex] x \approx 252 \\[3ex] $ The break-even point is approximately 252 books.
(2.) USSCE - Advance Mathematics Paper 1 The motion of a particle is described by the law $s(t) = t^3 - 2t^2 + t + 1$ where t is in seconds and s is in metres.
Its velocity after two (2) seconds is:

$ A.\;\; 5\;m/s \\[3ex] B.\;\; 3\;m/s \\[3ex] C.\;\; 1\;m/s \\[3ex] D.\;\; None\;\;of\;\;the\;\;above \\[3ex] $

$ Let\;\; velocity = v \\[3ex] s(t) = t^3 - 2t^2 + t + 1 \\[3ex] v = \dfrac{ds}{dt} = 3t^2 - 4t + 1 \\[3ex] After\;\;2\;\;seconds \implies t = 2 \\[3ex] v = 3(2)^2 - 4(2) + 1 \\[3ex] v = 12 - 8 + 1 \\[3ex] v = 5\;m/s $
(3.)

(4.) MEHA A women's club makes mats and sells them for $73 each.
The cost, in dollars, of making x mats is given by $C(x) = 3.6x^2 + x$
(a) What is the cost of making 15 mats?
(b) Find the formula for the profit made by selling x mats.
(c) Determine the number of mats the club should produce and sell to maximise its profit.


$ C(x) = cost\;\;function \\[3ex] R(x) = revenue\;\;function \\[3ex] P(x) = profit\;\;function \\[3ex] (a) \\[3ex] C(x) = 3.6x^2 + x \\[3ex] C(15) = 3.6(15)^2 + 15 \\[3ex] C(15) = 3.6(225) + 15 \\[3ex] C(15) = \$825.00 \\[3ex] (b) \\[3ex] R(x) = 73 * x = 73x \\[3ex] P(x) = R(x) - C(x) \\[3ex] P(x) = 73x - (3.6x^2 + x) \\[3ex] P(x) = 73x - 3.6x^2 - x \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] (c) \\[3ex] $ We can solve this question part using at least two approaches.
Vertex Method: the x-coordinate of the vertex gives the number of mats that should be sold to maximise the profit.
The y-coordinate of the vertex gives the maximum profit.

$ \underline{Vertex\;\;Method} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] a = -3.6,\;\; b = 72,\;\; c = 0 \\[3ex] x-coordinate\;\;of\;\;vertex \\[3ex] = -\dfrac{b}{2a} \\[5ex] = -\dfrac{72}{2(-3.6)} \\[5ex] = -\dfrac{72}{-7.2} \\[5ex] = 10 \\[3ex] $ 10 mats should be produced and sold to maximise profit.

$ \underline{Differential\;\;Calculus\;\;Approach} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] P'(x) = -7.2x + 72 \\[3ex] Set\;\;P'(x) = 0 \;\;and\;\;solve\;\;for\;\;x \\[3ex] -7.2x + 72 = 0 \\[3ex] -7.2x = -72 \\[3ex] x = \dfrac{-72}{-7.2} \\[5ex] x = 10 \\[3ex] $ 10 mats should be produced and sold to maximise profit.
(5.)


(6.) JAMB A trader realizes $10x - x^2$ naira profit from the sale of x bags of corn.
How many bags will give him the maximum profit?

$ A.\;\; 4 \\[3ex] B.\;\; 5 \\[3ex] C.\;\; 6 \\[3ex] D.\;\; 7 \\[3ex] $

We can do this question in at least two ways.
You may use any of the methods to solve it.

First Method: Vertex Formula: this is because the profit is a quadratic function
For this question:
the number of bags that will give the maximum profit = $x$ coordinate of the vertex
the maximum profit = $y$ coordinate of the vertex

$ y = 10x - x^2 \\[3ex] y = -x^2 + 10x \\[3ex] y = ax^2 + bx + c \\[3ex] a = -1, b = 10 \\[3ex] x-coordinate\:\: of\:\: Vertex = -\dfrac{b}{2a} \\[5ex] = \dfrac{-10}{2(-1)} \\[5ex] = \dfrac{-10}{-2} \\[5ex] = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.

Second Method: Differential Calculus
One of the application of derivatives is in calculating maxima and minima of functions
We need to review Differential Calculus before using this method.

$ y = 10x - x^2 \\[3ex] \dfrac{dy}{dx} = 10 - 2x \\[3ex] 10 - 2x = 0 \\[3ex] 10 = 2x \\[3ex] 2x = 10 \\[3ex] x = \dfrac{10}{2} \\[3ex] x = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.
(7.)


(8.)


(9.)

(10.)

(11.)

(12.)

(13.)

(14.)
(15.)


(16.)


(17.)

(18.)

(19.)


(20.)




Top


(21.)

(22.)

(23.)

(24.)

(25.)

(26.)

(27.)

(28.)