Quotes of the Day
If there is one prayer that you should pray/sing every day and every hour, it is the
LORD's prayer (Our FATHER in
Heaven prayer)
- Samuel Dominic Chukwuemeka
It is the most powerful prayer.
A pure heart, a clean mind, and a clear conscience is necessary for it.
For in GOD we live, and move, and have our being.
- Acts 17:28
The Joy of a Teacher is the Success of his Students.
- Samuel Dominic Chukwuemeka
Welcome to Our Site 😊

I greet you this day,
First: read the notes.
Second: view the videos.
Third: solve the questions/solved examples.
Fourth: check your solutions with my thoroughly-explained examples.
Fifth: Check your answers with the calculators.
I wrote the codes for the calculators using JavaScript, a client-side Scripting language.
Please use the latest Internet browsers. The calculators should work.
Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome. You may contact me.
If you are my student, please do not contact me here. Contact me via the school's system.
Thank you for visiting.
Samuel Dominic Chukwuemeka (Samdom For Peace)
B.Eng., A.A.T, M.Ed., M.S
Objectives
Students will:
(1.) Discuss vectors.
(2.) Discuss scalars.
(3.) Perform arithmetic operations on vectors.
(4.) Determine the angle between two vectors.
(5.) Solve problems involving vectors.
(6.) Solve applied problems on vectors.
Vocabulary Words
arrow, quantity, magnitude, absolute value, modulus, length, size, direction, vector, vector quantity, scalar, scalar quantity, distance, line, point, coordinates, x-coordinate, y-coordinate, initial point, head, terminal point, tail, origin, component form, horizontal component, vertical component, angle brackets, resultant, compass bearing, matrix, brackets, row, row vector, column, column vector, position vector, displacement vector, unit vector, component unit vectors, line vector, free vector, direction cosines, scalar product, dot product, vector product, cross product, direction ratios,
Definitions
A Vector or a Vector Quantity is a quantity that has magnitude and direction.
A Scalar or a Scalar Quantity is a quantity that has only magnitude.
It does not have direction.
A row vector is a matrix with only one row of elements.
A column vector is a matrix with only one column of elements.
A position vector is the vector that indicates the position of a point, say P with reference to the origin, O(0, 0).
In this case, it is denoted by $\overrightarrow{OP}$
A unit vector is a vector with a magnitude of 1 unit.
The unit vectors: i and j are used to express a vector in the horizontal axis (x-axis) and
vertical axis (y-axis) respectively.
Symbols and Formulas
(1.) A(x, y)
Point: A
(): parenthesis
x = x-coordinate
y = y-coordinate
(2.) A$\langle x, y \rangle$
Vector: A
$\langle \rangle$: angle brackets
x = horizontal component
y = vertical component
(3.) Given a vector: $\overrightarrow{AB}$
$
\overrightarrow{AB} = \vec{B} - \vec{A} \\[3ex]
first\;\;vector = \vec{A} = \langle A_x, A_y \rangle \\[3ex]
second\;\;vector = \vec{B} = \langle B_x, B_y \rangle \\[3ex]
\overrightarrow{AB} = \langle B_x - A_x, B_y - A_y \rangle \\[3ex]
\overrightarrow{BA} = -\overrightarrow{AB} \\[5ex]
$
(4.) Given a vector: $\overrightarrow{BA}$
$
first\;\;vector = \vec{B} = \langle B_x, B_y \rangle \\[3ex]
second\;\;vector = \vec{A} = \langle A_x, A_y \rangle \\[3ex]
\overrightarrow{BA} = \langle A_x - B_x, A_y - B_y \rangle \\[3ex]
\overrightarrow{AB} = -\overrightarrow{BA} \\[5ex]
$
(5.) Given several vectors:
Notice the colors and the pattern
$
(a.)\;\; \overrightarrow{AB} = -\overrightarrow{BA} \\[3ex]
(b.)\;\; \overrightarrow{CD} = -\overrightarrow{DC} \\[3ex]
(c.)\;\; \overrightarrow{A\color{red}{K}} + \overrightarrow{\color{red}{K}C} = \overrightarrow{AC} \\[3ex]
(d.)\;\; \overrightarrow{U\color{red}{K}} + \overrightarrow{\color{red}{K}S} = \overrightarrow{US} \\[3ex]
(e.)\;\; \overrightarrow{M\color{red}{P}} + \overrightarrow{\color{red}{P}C} + \overrightarrow{\color{red}{C}D} = \overrightarrow{MD} \\[5ex]
$
(6.) Given two position vectors: $\overrightarrow{OE}$ and $\overrightarrow{OF}$
$
\overrightarrow{EF} = \overrightarrow{EO} + \overrightarrow{OF} \\[3ex]
\overrightarrow{EF} = -\overrightarrow{OE} + \overrightarrow{OF} \\[5ex]
$
(7.) Given vectors in component form OR unit vectors:
Say for a two-dimensional vector A:
$
\boldsymbol{A}\langle x, y \rangle = x\boldsymbol{i} + y\boldsymbol{j} \\[3ex]
$
Say for a three-dimensional vector C:
$
\boldsymbol{C}\langle x, y, z \rangle = x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k} \\[3ex]
$
Sum and Difference of Vectors
Assume we have two two-dimensional vectors: C and D:
$
\boldsymbol{C}\langle c_1, c_2 \rangle = c_1\boldsymbol{i} + c_2\boldsymbol{j} \\[3ex]
\boldsymbol{D}\langle d_1, d_2 \rangle = d_1\boldsymbol{i} + d_2\boldsymbol{j} \\[5ex]
\underline{Sum} \\[3ex]
\vec{C} + \vec{D} \\[3ex]
= \langle c_1 + d_1, c_2 + d_2 \rangle \\[3ex]
= (c_1 + d_1)\boldsymbol{i} + (c_2 + d_2)\boldsymbol{j} \\[5ex]
\underline{Difference} \\[3ex]
\vec{C} - \vec{D} \\[3ex]
= \langle c_1 - d_1, c_2 - d_2 \rangle \\[3ex]
= (c_1 - d_1)\boldsymbol{i} + (c_2 - d_2)\boldsymbol{j} \\[5ex]
$
Assume we have two three-dimensional vectors: C and D:
$
\boldsymbol{C}\langle c_1, c_2, c_3 \rangle = c_1\boldsymbol{i} + c_2\boldsymbol{j} + c_3\boldsymbol{k} \\[3ex]
\boldsymbol{D}\langle d_1, d_2, d_3 \rangle = d_1\boldsymbol{i} + d_2\boldsymbol{j} + d_3\boldsymbol{j} \\[5ex]
\underline{Sum} \\[3ex]
\vec{C} + \vec{D} \\[3ex]
= \langle c_1 + d_1, c_2 + d_2, c_3 + d_3 \rangle \\[3ex]
= (c_1 + d_1)\boldsymbol{i} + (c_2 + d_2)\boldsymbol{j} + (c_3 + d_3)\boldsymbol{k} \\[5ex]
\underline{Difference} \\[3ex]
\vec{C} - \vec{D} \\[3ex]
= \langle c_1 - d_1, c_2 - d_2, c_3 - d_3 \rangle \\[3ex]
= (c_1 - d_1)\boldsymbol{i} + (c_2 - d_2)\boldsymbol{j} + (c_3 - d_3)\boldsymbol{k} \\[5ex]
$
Vectors
A Vector or a Vector Quantity is a quantity that has magnitude and direction.
It is denoted by any of these:
Vector A is denoted by $\vec{A}$ or the bold letter: A
Vector a is denoted by $\vec{a}$ or the bold letter: a
Vector AB is denoted by $\overrightarrow{AB}$ or the bold letters: AB
Vector BA is denoted by $\overrightarrow{BA}$ or the bold letters: BA
These are the basic representations.
Other representations are discussed below.
The magnitude of a vector quantity is the absolute value or the modulus of the quantity.
It is a value.
It has no sign. This means that it is neither positive nor negative.
The direction has a sign.
A plus sign indicates a positive direction.
A minus sign indicates a negative direction.
A Scalar or a Scalar Quantity is a quantity that has only magnitude.
It does not have direction.
Let us review several examples of vectors and scalars with explanations for such.
Note the different explanations.
If we cannot have negative values of the quantity, the quantity is a scalar.
If the formula of the quantity involves the dot product of only two vectors, it is a scalar because the dot product
of two vectors gives a scalar.
| Vectors | Scalars |
|---|---|
|
Time is the duration of events. It is a scalar. It has only magnitude...a nonnegative value. Time cannot be negative. |
|
|
Altitude is the height above sea level or ground level. The height of a body cannot be negative. It is a single value (magnitude) that has no direction. Therefore, altitude (height) is a scalar quantity. |
|
|
Displacement is a vector quantity because it is the distance (magnitude) with reference to a
specific direction. Positive direction is indicated by plus sign while negative direction is indicated by a minus sign. Examples: John walked 10 miles due east (+10 miles in the x-axis) to point A. Mark sailed 10 nautical miles due west (-10 miles in the x-axis) to point B. James ran 5 kilometers right of the building (+5 km) to point C. Jude drove 5 kilometers left of the building (-5 km) to point D. |
Distance between two items is how far apart between those items. It is the magnitude of the displacement. It does not specify the direction. It only specifies the magnitude. Examples: John walked 10 miles to point A. Mark sailed 10 nautical miles to point B. James ran 5 kilometers to point C. Jude drove 5 kilometers to point D. |
|
Velocity is a vector quantity because it is the rate of change of displacement. In other words, it is the quotient of the change in displacement and the change in time. The quotient of a vector and a scalar is a vector. It can have positive, zero, or negative values. |
Speed is a scalar because it is the rate of change of distance. It is the division of the change in distance and the change in time. The quotient of two scalars is a scalar. |
|
Acceleration is a vector quantity because it is the rate of change of velocity. In other words, it is the quotient of the change in velocity and the change in time. The quotient of a vector and a scalar is a vector. It can have positive, zero, or negative values. |
|
|
Mass of an item is the quantity of matter in the item. That quantity cannot be negative. It is a single value (magnitude) that has no direction. Mass is a scalar. |
|
|
Force is the product of the mass and the acceleration. Mass is a scalar. Acceleration is a vector. The product of a scalar and a vector is a vector. Force is a vector. |
|
|
Weight is the force of gravity on a body. It is a vector quantity. |
|
|
Energy or Work is the dot product of force and displacement. Force is a vector. Displacement is a vector. But the dot product of two vectors is a scalar. Enery is a scalar quantity. |
|
|
Temperature is a scalar quantity. But why? Temperature has positive, zero, and negative values. Why is it scalar? Because it has no direction. The negative value, zero value, or positive value of a temperature is the actual value of that temperature. In this case, a negative value does not signify direction. |
Representation of Vectors
A vector can be represented:
(1.) On a Graph as a Line
The length of the linerepresents the magnitudeof the vector.
The direction of the line represents the direction in which the vector acts.
An arrowhead indicates the sense of the direction.
In this case, the line on the graph has two points
One end of the line is the initial point (also known as the head).
The initial point is a dot.
The other end of the line is the terminal point (also known as the tail).
The terminal point is an arrow.
A point (x, y) has two coordinates: the x-coordinate and the y-coordinate
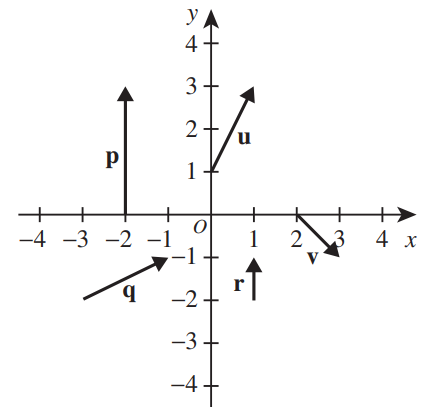
Example: In the graph below, u, v, p, q and r are vectors.
(2.) In Component Form
This is the representation of a vector using angle brackets $\langle x, y \rangle$
To express a vector represented by a line on a graph into component form,
there are at least two approaches we can use.
We shall discuss the first approach here and discuss the second approach in Number (3.)
First Approach: Subtraction of Point Coordinates
(a.) Note the initial point of the vector
(b.) Note the terminal point of the vector
(c.) Subtract the x-coordinate of the initial point from the x-coordinate of the terminal point
(d.) Subtract the y-coordinate of the initial point from the y-coordinate of the terminal point
(e.) Express the vector in component form
NOTE: If the initial point of the vector is the origin (0, 0), then the component form of the vector is the terminal
point expressed in angle brackets.
This is because the subtraction of the origin from the terminal point still gives the terminal point.
It is necessary you include the angle brackets in order to show that it is a vector, and not a point.
Let us express all the vectors in the graph in component form
$
\underline{vector\;\;u} \\[3ex]
initial\;\;point = (0, 1) \\[3ex]
terminal\;\;point = (1, 3) \\[3ex]
u: (0, 1) \rightarrow (1, 3) \\[3ex]
u: \langle 1 - 0, 3 - 1 \rangle \\[3ex]
u \langle 1, 2 \rangle \\[3ex]
\underline{vector\;\;v} \\[3ex]
initial\;\;point = (2, 0) \\[3ex]
terminal\;\;point = (3, -1) \\[3ex]
v: (2, 0) \rightarrow (3, -1) \\[3ex]
v: \langle 3 - 2, -1 - 0 \rangle \\[3ex]
v \langle 1, -1 \rangle \\[3ex]
\underline{vector\;\;p} \\[3ex]
initial\;\;point = (-2, 0) \\[3ex]
terminal\;\;point = (-2, 3) \\[3ex]
p: (-2, 0) \rightarrow (-2, 3) \\[3ex]
p: \langle -2 - (-2), 3 - 0 \rangle \\[3ex]
p: \langle -2 + 2, 3 \rangle \\[3ex]
p \langle 0, 3 \rangle \\[3ex]
\underline{vector\;\;q} \\[3ex]
initial\;\;point = (-3, -2) \\[3ex]
terminal\;\;point = (-1, -1) \\[3ex]
q: (-3, -2) \rightarrow (-1, -1) \\[3ex]
q: \langle -1 - (-3), -1 - (-2) \rangle \\[3ex]
q: \langle -1 + 3, -1 + 2 \rangle \\[3ex]
q \langle 2, 1 \rangle \\[3ex]
\underline{vector\;\;r} \\[3ex]
initial\;\;point = (1, -2) \\[3ex]
terminal\;\;point = (1, -1) \\[3ex]
r: (1, -2) \rightarrow (1, -1) \\[3ex]
r: \langle 1 - 1, -1 - (-2) \rangle \\[3ex]
r: \langle 0, -1 + 2 \rangle \\[3ex]
r \langle 0, 1 \rangle \\[3ex]
$
(3.) As a Matrix
Any vector expressed as a point or in component form can also be expressed as a row vector and column vector
A row vector is a matrix with only one row of elements.
A column vector is a matrix with only one column of elements.
For the row vector, the horizontal component is written before the vertical component from left to right.
For the column vector, the horizontal component is written before the vertical component from top to bottom.
Let us do an example.
Example: Here is vector a.
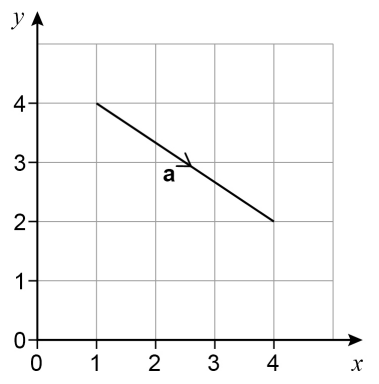
Determine the row vector and the column vector of a
$
\underline{First\;\;Approach:\;\;Subtraction\;\;of\;\;Point\;\;Coordinates} \\[3ex]
Initial\;\;point = (1, 4) \\[3ex]
Terminal\;\;point = (4, 2) \\[3ex]
a: (1, 4) \rightarrow (4, 2) \\[3ex]
a: \langle 4 - 1, 2 - 4 \rangle \\[3ex]
a \langle 3, -2 \rangle \\[3ex]
Row\;\;vector = [3\;\;\;-2] \\[3ex]
Column\;\;vector =
\begin{bmatrix}
3 \\[3ex]
-2
\end{bmatrix}
$
Let us discuss another approach that we can use to solve the question
Second Approach: Counting
For an inclined line (line inclined at an angle):
(1.) Locate the point of intersection needed to form a right triangle from the initial point to the terminal point.
(2.) Complete a right triangle from the initial point to the terminal point.
(3.) Count the number of vertical steps from the initial point to the point of intersection.
If you count from top to bottom, the count is negative (falling).
If you count from bottom to top, the count is positive (rising).
Compare to positive slope (rising) and negative slope (falling).
That number is the vertical component of the vector.
(4.) Count the number of horizontal steps from the point of intersection to the terminal point.
If you count from right to left, the count is negative (backward).
If you count from left to right, the count is positive (forward).
That number is the horizontal component of the vector.
For a vertical line:
Count the number of vertical steps from the initial point to the terminal point.
That number is the vertical component of the vector.
The horizontal component of the vector is zero.
For a horizontal line:
Count the number of horizontal steps from the initial point to the terminal point.
That number is the horizontal component of the vector.
The vertical component of the vector is zero.
Let us do the same example using the Counting Method/Approach
Let:
black = point of intersection
red = vertical
darkblue = horizontal
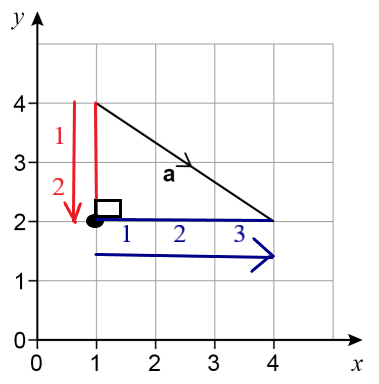
$
bottom-to-top:\;\; y = -2 \\[3ex]
left-to-right:\;\; x = 3 \\[3ex]
a \langle x, y \rangle = a \langle 3, -2 \rangle \\[3ex]
Row\;\;vector = [3\;\;\;-2] \\[3ex]
Column\;\;vector =
\begin{bmatrix}
3 \\[3ex]
-2
\end{bmatrix} \\[3ex]
$
(4.) As a Position Vector
A position vector is the vector that indicates the position of a point, say P with reference to the origin, O(0, 0).
In this case, it is denoted by $\overrightarrow{OP}$
This implies that the direction of the position vector always points from the origin towards the point.
(5.) Using unit vectors: i, j and k
A unit vector is a vector with a magnitude of 1 unit.
The unit vectors: i and j are used to express a vector in the horizontal axis (x-axis) and
vertical axis (y-axis) respectively.
Say for vector A:
$\boldsymbol{A}\langle x, y \rangle = x\boldsymbol{i} + y\boldsymbol{j}$
Say for vector C:
$\boldsymbol{C}\langle x, y, z \rangle = x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k}$
For any representation:
(A.) The maginude of a vector is the distance between the initial point and the terminal point.
(B.) The maginude of a vector is the length or size of the vector.
(C.) The magnitude of a vector is the distance of the vector from the origin.
(D.) The direction of a vector is the direction of the vector from the origin.
References
Chukwuemeka, S.D (2022, April 30). Samuel Chukwuemeka Tutorials - Math, Science, and Technology.
Retrieved from https://www.samuelchukwuemeka.com
Authority (NZQA), (n.d.). Mathematics and Statistics subject resources. www.nzqa.govt.nz. Retrieved June 14,
2022, from https://www.nzqa.govt.nz/ncea/subjects/mathematics/levels/
CrackACT. (n.d.). Retrieved from http://www.crackact.com/act-downloads/
CSEC Math Tutor. (n.d). Retrieved from https://www.csecmathtutor.com/past-papers.html
DLAP Website. (n.d.). Curriculum.gov.mt.
https://curriculum.gov.mt/en/Examination-Papers/Pages/list_secondary_papers.aspx
Elementary, Intermediate Tests and High School Regents Examinations : OSA : NYSED. (2019).
Nysedregents.org. https://www.nysedregents.org/
Free Jamb Past Questions And Answer For All Subject 2020. (2022, January 31). Vastlearners.
https://www.vastlearners.com/free-jamb-past-questions/
GCSE and SQA Exam Past Papers: Revision World. Retrieved April 6, 2022, from
https://revisionworld.com/gcse-revision/gcse-exam-past-papers
JAMB Past Questions, WAEC, NECO, Post UTME Past Questions. (n.d.). Nigerian Scholars. Retrieved February 12, 2022,
from https://nigerianscholars.com/past-questions/
K.C.S.E PAST PAPERS 1996 - 2021. (n.d.). Teacher.co.ke. https://teacher.co.ke/k-c-s-e-past-papers-1996-2021/
Myschool e-Learning Centre - It’s Time to Study! - Myschool. (n.d.). https://myschool.ng/classroom
Netrimedia. (2022, May 2). ICSE 10th Board Exam Previous Papers- Last 10 Years. Education Observer.
https://www.educationobserver.com/icse-class10-previous-papers/
NSC Examinations. (n.d.). www.education.gov.za.
https://www.education.gov.za/Curriculum/NationalSeniorCertificate(NSC)Examinations.aspx
Papua New Guinea: Department of Education. (n.d.). www.education.gov.pg.
https://www.education.gov.pg/TISER/exams.html
West African Examinations Council (WAEC). Retrieved May 30, 2022, from
https://waeconline.org.ng/e-learning/Mathematics/mathsmain.html